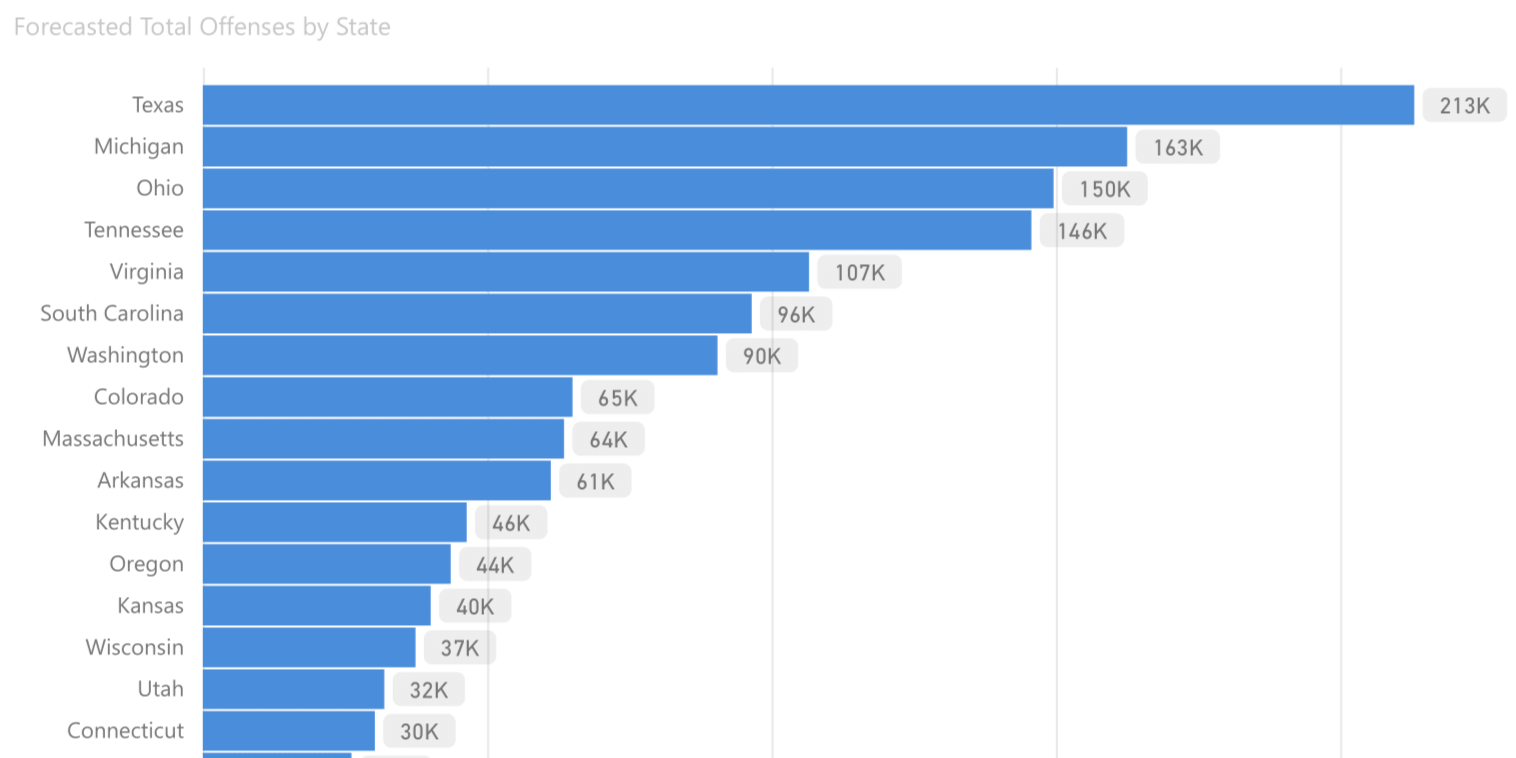
Total Offenses
The cleaned dataset, used for 'Total Offenses' contained an actual count of 1,725,358. This 'apples-to-apples' comparison, based on the sum of errors (MAE), rather than the error of the sum, resulted in the autoregression model having a forecasting accuracy of 91.69%, with an average forecasting error of -4.53% by state.
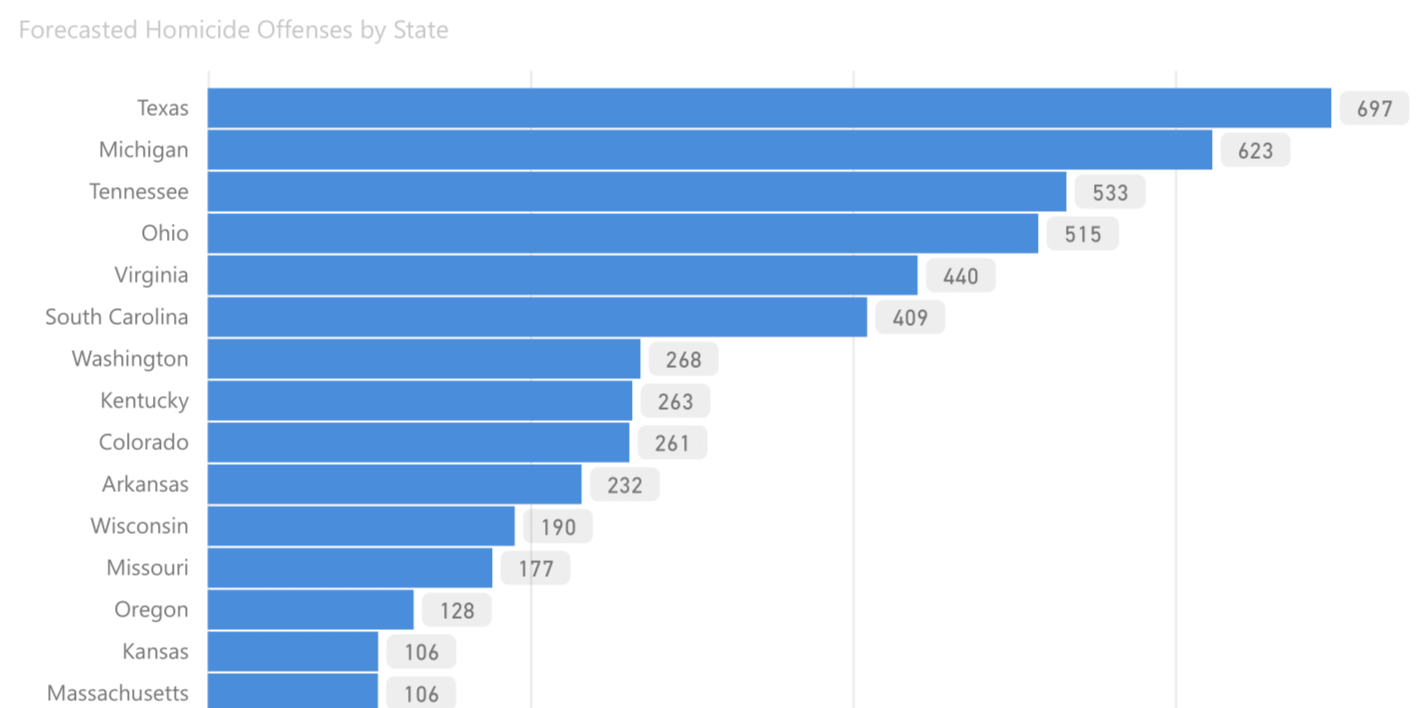
Forecasting Count by State
Forecasting Stats

Homicide Offenses
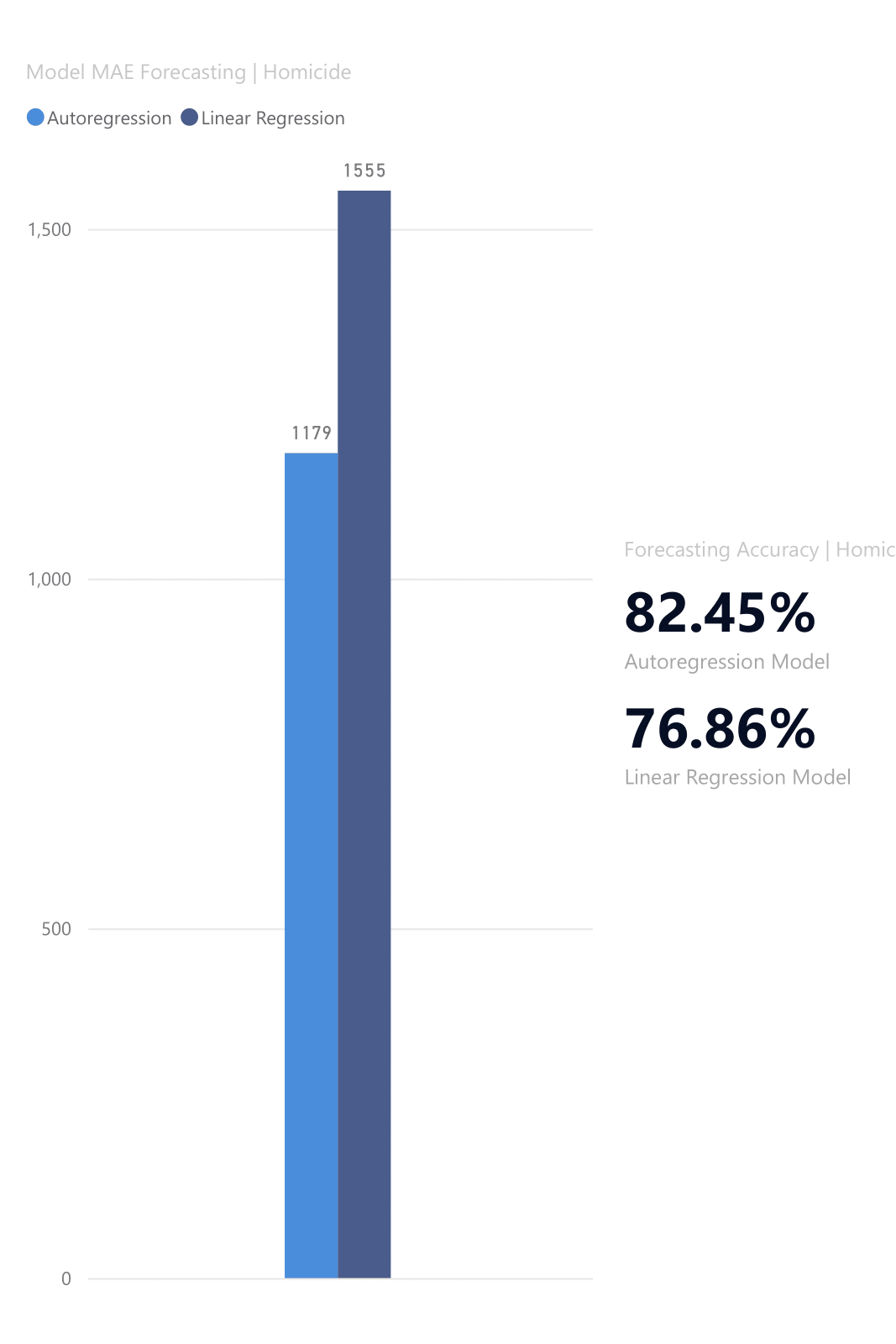
The cleaned dataset, used for 'Homicide Offenses' contained an actual count of 6,719. This 'apples-to-apples' comparison, based on the sum of errors (MAE), rather than the error of the sum, resulted in the autoregression model having a forecasting accuracy for Homicide Offenses at 82.45%, with an average forecasting error of -13.96% by state.

Linear VS Autoregression Model Accuracy
The Autoregression Model was selected as the final forecasting methodology due to its superior performance in predicting 2019 crime statistics. Compared to Linear Regression, the Autoregressive approach improved accuracy by 8.02 percentage points for Total Offenses and 5.59 percentage points for Homicide Offenses. While these margins may appear nominal, the Mean Absolute Error (MAE) reveals a significant gap in predictive reliability and model magnitude. A detailed performance analysis follows below.
Total Offense Forecast

Homicide Offense Forecast
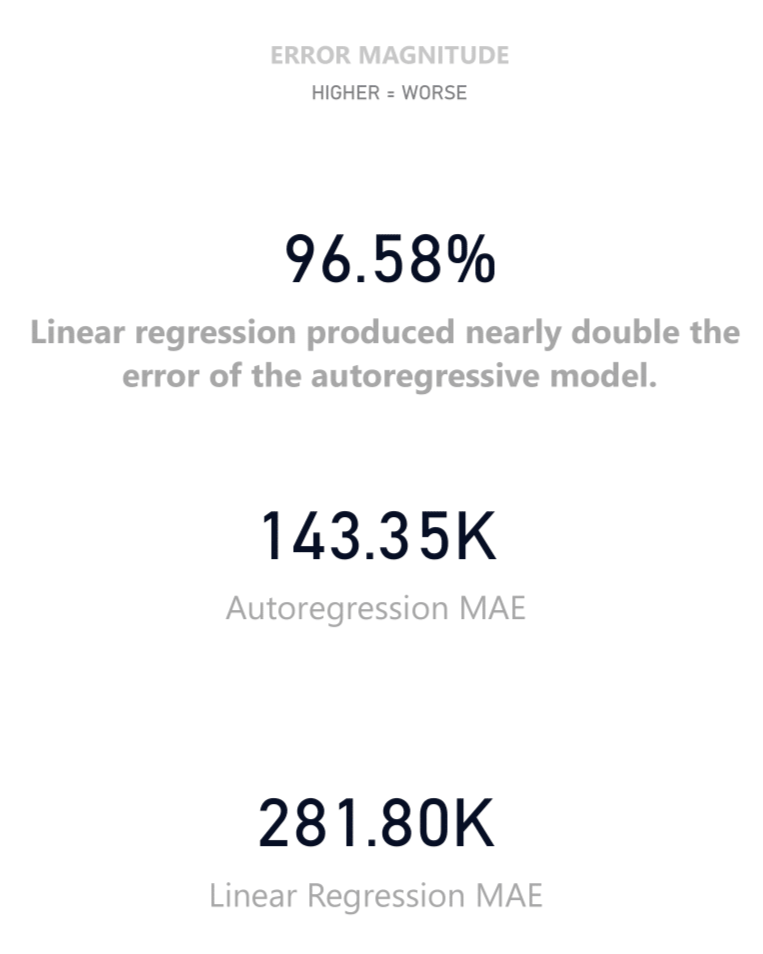
Understanding Error Magnitude & MAE
A surface-level comparison of accuracy metrics (91.69% vs 83.67%) disguises the true
performance gap between the two models.
By examining the inverse metric, the Error Rate, we see that the Linear Regression
Model (16.33%) produced nearly twice as many errors as the Autoregression Model
(8.31%).
This is then confirmed by the Mean Absolute Error (MAE), which shows the Linear
Model's total error magnitude was 96.58% greater than the Autoregressive approach.
In short: The 8-point gap in accuracy resulted in a double-magnitude gap in
reliability.
Total Offense Forecast
Homicide Offense Forecast

Mathematical Breakdown: Why 8% Accuracy Difference = 96% More Error
| Metric | Autoregression (AR) | Linear Regression (LR) |
|---|---|---|
| Forecast Accuracy | 91.69% | 83.67% |
| Calculate Error Rate | 100% - 91.69% = 8.31% | 100% - 83.67% = 16.33% |
| Error Rate | 8.31% | 16.33% (Nearly Double) |
| Mean Absolute Error (MAE) | 143,350 | 281,800 |
The Calculation:
((Linear MAE - AR MAE) / AR MAE) * 100
((281,800 - 143,350) / 143,350) * 100 = 96.58% Increase in Error